
In the realm of mathematics, understanding how to multiply and divide fractions is a fundamental skill that forms the backbone of countless complex calculations. These operations empower us to solve real-world problems, ranging from determining the area of a rectangular prism to calculating the speed of a moving object. By mastering the art of fraction multiplication and division, we unlock a gateway to a world of mathematical possibilities.
To embark on this mathematical journey, let us delve into the world of fractions. A fraction represents a part of a whole, expressed as a quotient of two integers. The numerator, the integer above the fraction bar, indicates the number of parts being considered, while the denominator, the integer below the fraction bar, represents the total number of parts in the whole. Understanding this concept is paramount as we explore the intricacies of fraction multiplication and division.
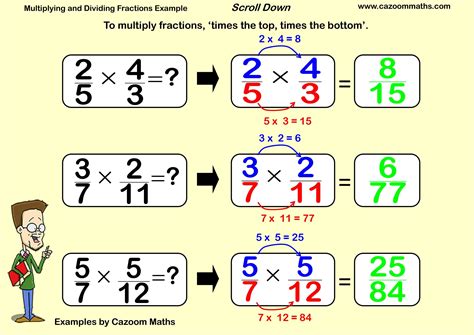
To multiply fractions, we embark on a straightforward process. We simply multiply the numerators of the fractions and the denominators of the fractions, respectively. For instance, multiplying 1/2 by 3/4 results in 1 × 3 / 2 × 4, which simplifies to 3/8. This intuitive method enables us to combine fractions, representing the product of the parts they represent. Conversely, division of fractions invites a slight twist: we invert the second fraction (the divisor) and multiply it by the first fraction. To illustrate, dividing 1/2 by 3/4 involves inverting 3/4 to 4/3 and multiplying it by 1/2, resulting in 1/2 × 4/3, which simplifies to 2/3. This inverse operation allows us to determine how many times one fraction contains another.
The Purpose of Multiplying Fractions
Multiplying fractions has various practical applications in everyday life and across different fields. Here are some key reasons why we use fraction multiplication:
1. Scaling Quantities: Multiplying fractions allows us to scale quantities proportionally. For instance, if we have 2/3 of a pizza, and we want to serve half of it to a friend, we can calculate the amount we need to give them by multiplying 2/3 by 1/2, resulting in 1/3 of the pizza.
| Original Amount |
Fraction to Scale |
Result |
| 2/3 pizza |
1/2 |
1/3 pizza |
2. Calculating Rates and Densities: Multiplying fractions is essential for determining rates and densities. Velocity, for example, is calculated by multiplying distance by time, which often involves multiplying fractions (e.g., miles per hour). Similarly, density is calculated by multiplying mass by volume, which can also involve fractions (e.g., grams per cubic centimeter).
3. Solving Proportions: Fraction multiplication plays a vital role in solving proportions. Proportions are equations that state that two ratios are equal. We use fraction multiplication to find the unknown term in a proportion. For example, if we know that 2/3 is equivalent to 8/12, we can multiply 2/3 by a factor that makes the denominator equal to 12, which in this case is 4.
2. Step-by-Step Process
Multiplying the Numerators and Denominators
The first step in multiplying fractions is to multiply the numerators of the two fractions together. The resulting number becomes the numerator of the answer. Similarly, multiply the denominators together. This result becomes the denominator of the answer.
For example, let’s multiply 1/2 by 3/4:
| Numerators: |
1 * 3 = 3 |
| Denominators: |
2 * 4 = 8 |
The product of the numerators is 3, and the product of the denominators is 8. Therefore, 1/2 * 3/4 = 3/8.
Simplifying the Product
After multiplying the numerators and denominators, check if the result can be simplified. Look for common factors between the numerator and denominator and divide them out. This will produce the simplest form of the answer.
In our example, 3/8 cannot be simplified further because there are no common factors between 3 and 8. Therefore, the answer is simply 3/8.
The Significance of Dividing Fractions
Dividing fractions is a fundamental operation in mathematics that plays a crucial role in various real-world applications. From solving everyday problems to complex scientific calculations, dividing fractions is essential for understanding and manipulating mathematical concepts. Here are some of the primary reasons why dividing fractions is important:
Problem-Solving in Daily Life
Dividing fractions is often encountered in practical situations. For instance, if a recipe calls for dividing a cup of flour evenly among six people, you need to divide 1/6 of the cup by 6 to determine how much each person receives. Similarly, dividing a pizza into equal slices or apportioning ingredients for a batch of cookies involves using division of fractions.
Measurement and Proportions
Dividing fractions is vital in measuring and maintaining proportions. In construction, architects and engineers use fractions to represent measurements, and dividing fractions allows them to calculate ratios for precise proportions. Similarly, in science, proportions are often expressed as fractions, and dividing fractions helps determine the concentration of substances in solutions or the ratios of ingredients in chemical reactions.
Real-World Calculations
Division of fractions finds applications in diverse fields such as finance, economics, and physics. In finance, calculating interest rates, currency exchange rates, or investment returns involves dividing fractions. In economics, dividing fractions helps analyze production rates, consumption patterns, or price-to-earnings ratios. Physicists use division of fractions when working with energy, velocity, or force, as these quantities are often expressed as fractions.
Overall, dividing fractions is a vital mathematical operation that enables us to solve problems, make measurements, maintain proportions, and perform complex calculations in various real-world scenarios.
The Step-by-Step Process of Dividing Fractions
Step 1: Determine the Reciprocal of the Second Fraction
To divide two fractions, you need to multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply the flipped fraction. For example, the reciprocal of 1/2 is 2/1.
Step 2: Multiply the Numerators and Multiply the Denominators
Once you have the reciprocal of the second fraction, you can multiply the numerators and multiply the denominators of the two fractions. This will give you the numerator and denominator of the resulting fraction.
Step 3: Simplify the Fraction (Optional)
The final step is to simplify the fraction if possible. This means dividing the numerator and denominator by their greatest common factor (GCF). For example, the fraction 6/8 can be simplified to 3/4 by dividing both the numerator and denominator by 2.
Step 4: Additional Examples
Let’s practice with a few examples:
| Example |
Step-by-Step Solution |
Result |
| 1/2 ÷ 1/4 |
1/2 x 4/1 = 4/2 = 2 |
2 |
| 3/5 ÷ 2/3 |
3/5 x 3/2 = 9/10 |
9/10 |
| 4/7 ÷ 5/6 |
4/7 x 6/5 = 24/35 |
24/35 |
Remember, dividing fractions is simply a matter of multiplying by the reciprocal and simplifying the result. With a little practice, you’ll be able to divide fractions with ease!
Common Errors in Multiplying and Dividing Fractions
Multiplying and dividing fractions can be tricky, and it’s easy to make mistakes. Here are some of the most common errors that students make:
1. Not simplifying the fractions first.
Before you multiply or divide fractions, it’s important to simplify them first. This means reducing them to their lowest terms. For example, 2/4 can be simplified to 1/2, and 3/6 can be simplified to 1/2.
2. Not multiplying the numerators and denominators separately.
When you multiply fractions, you multiply the numerators together and the denominators together. For example, (2/3) * (3/4) = (2 * 3) / (3 * 4) = 6/12.
3. Not dividing the numerators by the denominators.
When you divide fractions, you divide the numerator of the first fraction by the denominator of the second fraction, and then divide the denominator of the first fraction by the numerator of the second fraction. For example, (2/3) / (3/4) = (2 * 4) / (3 * 3) = 8/9.
4. Not multiplying the fractions in the correct order.
When you multiply fractions, it doesn’t matter which order you multiply them in. However, when you divide fractions, it does matter. You must always divide the first fraction by the second fraction.
5. Not checking your answer.
Once you’ve multiplied or divided fractions, it’s important to check your answer to make sure it’s correct. You can do this by multiplying the answer by the second fraction (if you multiplied) or dividing the answer by the second fraction (if you divided). If you get the original fraction back, then your answer is correct.
Here are some examples of how to correct these errors:
| Error |
Correction |
| 2/4 * 3/4 = 6/8 |
2/4 * 3/4 = (2 * 3) / (4 * 4) = 6/16 |
| 3/4 / 3/4 = 1/1 |
3/4 / 3/4 = (3 * 4) / (4 * 3) = 1 |
| 4/3 / 3/4 = 4/3 * 4/3 |
4/3 / 3/4 = (4 * 4) / (3 * 3) = 16/9 |
| 2/3 * 3/4 = 6/12 |
2/3 * 3/4 = (2 * 3) / (3 * 4) = 6/12 = 1/2 |
Applications of Multiplying and Dividing Fractions
Fractions are a fundamental part of mathematics and have numerous applications in real-world scenarios. Multiplying and dividing fractions is crucial in various fields, including:
Calculating Rates
Fractions are used to represent rates, such as speed, density, or flow rate. Multiplying or dividing fractions allows us to calculate the total amount, distance traveled, or volume of a substance.
Scaling Recipes
When adjusting recipes, we often need to multiply or divide the ingredient amounts to scale up or down the recipe. By multiplying or dividing the fraction representing the amount of each ingredient by the desired scale factor, we can ensure accurate proportions.
Measurement Conversions
Converting between different units of measurement often involves multiplying or dividing fractions. For instance, to convert inches to centimeters, we multiply the number of inches by the fraction representing the conversion factor (1 inch = 2.54 centimeters).
Probability Calculations
Fractions are used to represent the probability of an event. Multiplying or dividing fractions allows us to calculate the combined probability of multiple independent events.
Calculating Proportions
Fractions represent proportions, and multiplying or dividing them helps us determine the ratio between different quantities. For example, in a recipe, the fraction of flour to butter represents the proportion of each ingredient needed.
Tips for Multiplying Fractions
When multiplying fractions, multiply the numerators and multiply the denominators:
|
Numerators |
Denominators |
| Initial Fraction |
a / b |
c / d |
| Multiplied Fraction |
a * c / b * d |
/ |
Tips for Dividing Fractions
When dividing fractions, invert the second fraction (divisor) and multiply:
|
Numerators |
Denominators |
| Initial Fraction |
a / b |
c / d |
| Inverted Fraction |
c / d |
a / b |
| Multiplied Fraction |
a * c / b * d |
/ |
Tips for Simplifying Fractions After Multiplication
After multiplying or dividing fractions, simplify the result to its lowest terms by finding the greatest common factor (GCF) of the numerator and denominator. There are several ways to do this:
- Prime factorization: Write the numerator and denominator as a product of their prime factors, then cancel out the common ones.
- Factoring using difference of squares: If the numerator and denominator are perfect squares, use the difference of squares formula (a² – b²) = (a + b)(a – b) to factor out the common factors.
- Use a calculator: If the numbers are large or the factoring process is complex, use a calculator to find the GCF.
Example: Simplify the fraction (8 / 12) * (9 / 15):
1. Multiply the numerators and denominators: (8 * 9) / (12 * 15) = 72 / 180
2. Factor the numerator and denominator: 72 = 23 * 32, 180 = 22 * 32 * 5
3. Cancel out the common factors: 22 * 32 = 36, so the simplified fraction is 72 / 180 = 36 / 90 = 2 / 5
Converting Mixed Numbers to Fractions for Division
When dividing mixed numbers, it’s necessary to convert them to improper fractions, where the numerator is larger than the denominator.
To do this, multiply the whole number by the denominator and add the numerator. The result becomes the new numerator over the same denominator.
For example, to convert 3 1/2 to an improper fraction, we multiply 3 by 2 (the denominator) and add 1 (the numerator):
“`
3 * 2 = 6
6 + 1 = 7
“`
So, 3 1/2 as an improper fraction is 7/2.
Additional Details
Here are some additional details to consider when converting mixed numbers to improper fractions for division:
- Negative mixed numbers: If the mixed number is negative, the numerator of the improper fraction will also be negative.
- Improper fractions with different denominators: If the mixed numbers to be divided have different denominators, find the least common multiple (LCM) of the denominators and convert both fractions to improper fractions with the LCM as the common denominator.
- Simplifying the improper fraction: After converting the mixed numbers to improper fractions, simplify the resulting improper fraction, if possible, by finding common factors and dividing both the numerator and denominator by the common factor.
| Mixed Number |
Improper Fraction |
| 2 1/3 |
7/3 |
| -4 1/2 |
-9/2 |
| 5 3/5 |
28/5 |
The Reciprocal Rule for Dividing Fractions
When dividing fractions, we can use the reciprocal rule. This rule states that the reciprocal of a fraction (a/b) is (b/a). For example, the reciprocal of 1/2 is 2/1 or simply 2.
To divide fractions using the reciprocal rule, we:
- Flip the second fraction (the divisor) to make the reciprocal.
- Multiply the numerators and the denominators of the two fractions.
For example, let’s divide 3/4 by 5/6:
3/4 ÷ 5/6 = 3/4 × 6/5
Applying the multiplication:
3/4 × 6/5 = (3 × 6) / (4 × 5) = 18/20
Simplifying, we get:
18/20 = 9/10
Therefore, 3/4 ÷ 5/6 = 9/10.
Here’s a table summarizing the steps for dividing fractions using the reciprocal rule:
| Step |
Description |
| 1 |
Flip the divisor (second fraction) to make the reciprocal. |
| 2 |
Multiply the numerators and denominators of the two fractions. |
| 3 |
Simplify the result if possible. |
Fraction Division as a Reciprocal Operation
When dividing fractions, you can use a reciprocal operation. This means you can flip the fraction you’re dividing by upside down, and then multiply. For example:
“`
3/4 ÷ 1/2 = (3/4) * (2/1) = 6/4 = 3/2
“`
The reason this works is because division is the inverse operation of multiplication. So, if you divide a fraction by another fraction, you’re essentially multiplying the first fraction by the reciprocal of the second fraction.
Steps for Dividing Fractions Using the Reciprocal Operation:
1. Flip the fraction you’re dividing by upside down. This is called finding the reciprocal.
2. Multiply the first fraction by the reciprocal.
3. Simplify the resulting fraction, if possible.
Example:
“`
Divide 3/4 by 1/2:
3/4 ÷ 1/2 = (3/4) * (2/1) = 6/4 = 3/2
“`
Table:
| Fraction |
Reciprocal |
| 3/4 |
4/3 |
| 1/2 |
2/1 |
How to Multiply and Divide Fractions
Multiplying fractions is easy! Just multiply the numerators (the top numbers) and the denominators (the bottom numbers) of the fractions.
For example:
To multiply 1/2 by 3/4, we multiply 1 by 3 and 2 by 4, which gives us 3/8.
Dividing fractions is also easy. To divide a fraction, we flip the second fraction (the divisor) and multiply. That is, we multiply the numerator of the first fraction by the denominator of the second fraction, and the denominator of the first fraction by the numerator of the second fraction.
For example:
To divide 1/2 by 3/4, we flip 3/4 and multiply, which gives us 4/6, which simplifies to 2/3.
People Also Ask
Can we add fractions with different denominators?
Yes, we can add fractions with different denominators by first finding the least common multiple (LCM) of the denominators. The LCM is the smallest number that is divisible by all the denominators.
For example:
To add 1/2 and 1/3, we first find the LCM of 2 and 3, which is 6. Then, we rewrite the fractions with the LCM as the denominator:
1/2 = 3/6
1/3 = 2/6
Now we can add the fractions:
3/6 + 2/6 = 5/6